再探PBR--微表面模型

还记得面试被问到是否了解PBR的时候，我每次都能吟唱而出：“PBR基于能量守恒理论，能保证入射能量和出射能量一致，其中，漫反射由Lambert项模拟，而金属材质由Cook-Torrance项模拟，Cook-Torrance基于微表面模型包括法线分布，几何遮蔽以及菲涅尔反射项。”每当被问到这些问题，我心里都在祈祷面试官不会继续追问下去，因为我并不清楚这几个神奇的式子究竟是从哪里冒出来的，和它声称的“微表面”模型的联系在哪里（实际上工业界可能确实不关心这些问题）。

最近刷了一下UCSD CSE 272，并阅读了Eric[1]，在这方面又有些新的感悟，随撰文记录。

1.再探微表面模型

微表面模型假设了物体表面由无数微小表面构成的，这些微小表面的表现累积成了宏观上物体表面的表现。目前，网上很多流行的PBR教程都是这么描述的。然而，目前鲜有资料说明用更严谨的数学语言描述这些微表面的行为，微表面模型中法线分布D, 菲涅尔F以及几何遮蔽项G这些描述宏观统计表现的项是怎么”统计”出来的。而这就是本节的重点。

考虑一个微表面分布，如图1所示。

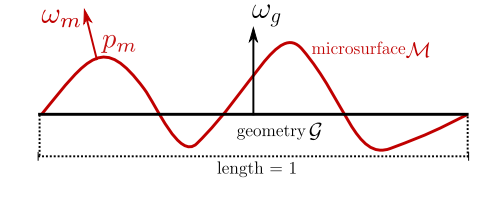
对于一个法线为 的物体表面（黑色线段），其由无数微表面构成（红色曲线段）。其中，微表面上任意一点 的法线为 。假设物体表面 为单位面积1 ，则红色微表面在物体表面上的投影面积必须与其相等，如公式(1)所示。

$$\int w_g\cdot w_m dp_m = 1 (1)$$

由了以上定义，我们可以定义法线分布(Distribution of Normal)。该项统计了在物体表面上朝向指定方向的微表面法线占整个区域的面积。如公式(2)所示。

$$D(w) = \int_M \delta_w(w_m(p_m)) dp_m (2)$$

其中， 为采样函数。 为整个微表面区域(图中红色线)。通过公式(2)，可以算出法向为 的微表面的面积总和。

在Eric[1]原文中，特意强调了这里Distribution of Normal与Normal Distribution的差异。但在后文关于BRDF的推导中，又直接使用这里的Distribution of Normal作为BRDF方程中的Normal Distribution，导致一定歧义。个人认为，Distribution of Normal与Normal Distribution主要在于一个是在确定面积下的确定面积量，一个是无限小微元上的密度，两者在一定程度上是等价的。

此外，考虑一块微表面区域 ，以及单位圆上的一块区域 满足 中的任意一点 对应的法线 有 。且对于任意 存在 。两者存在几何关系，如公式(3)所示。

$$A=\int_{M'} dp_m = \int_{\Omega'} D(w_m) dw_m(3)$$

其中，A为 微表面区域面积。该关系可以通过积分换序证得，如公式(4)所示。

$$\int_{\Omega'} D(w_m) dw_m=\int_{\Omega'} \int_{M'} \delta_{w_m}(w_m) dp_mdw_m=\int_{M'}\int_{\Omega'}\delta_{w_m}(w_m) dw_m dp_m=\int_{M'} dp_m (4)$$

同样的对于定义在方向角上的任意函数 ，其同样满足类似公式(3)的关系。如公式(5)所示。

$$\int_{\Omega'} f(w_m) D(w_m) dw_m = \int_{M'} f(w_m(p_m))dp_m (5)$$

公式(5)的证明过程和公式(4)类似，这里不再赘述。

而对于定义在微表面上的任意函数 ，则可以通过公式(6)定义其在方向角空间下的对应形式。

$$g(w) = \frac{\int_{M'} g(p_m)\delta_{w}(w_m(p_m))dp_m }{\int_{M'} \delta_{w}(w_m(p_m))dp_m} (6)$$

将其带入到公式(7)中便可验证。

$$\int_{\Omega'} g(w_m) D(w_m)dw_m = \int_{\Omega'} \frac{\int_{M'} g(p_m) \delta_{w_m}(w_m(p_m))dp_m}{D(w_m)} D(w_m) dw_m$$ $$= \int_{\Omega'} \int_{M'} g(p_m) \delta_{w_m}(w_m(p_m))dp_mdw_m=\int_{M'}g(p_m)dp_m (7)$$

公式(6)提供了统计了微表面中的某项属性并将其转到宏观表面尺度，进而使微表面模型转为我们可以计算的宏观表面模型。

2.从微表面模型到BRDF

本节将从微表面模型建立对应的宏观BRDF模型。

首先考虑对于物体表面 其出射辐射度可以表示为公式(8):

$$L(w_0, M) = \frac{\int_M Proj(p_m,w_o) L(w_o, p_m) dp_m}{\int_M Proj(p_m,w_o)dp_m} (8)$$

其中 为从各个微表面中出射的辐射度，而 为微表面投影到视线方向 上后的面积。如图2所示，红色区域中的微表面通过 操作被投影到绿色区域上。由于辐射度的物理含义为物体表面向某方向出射能量的密度，因此公式(8)分子通过计算辐射度关于面积的加权求和计算对应区域的辐照度，除以分母宏观区域的投影面积后，得到投影后的辐射度。

在图2中，可以观察到微表面存在自成阴影的黑色区域，而这些黑色区域是不对最终的投影面积做贡献。因此，可以考虑在投影项 中加入几何遮蔽项 描述这一现象。当微表面处于未遮蔽区域时，其几何遮蔽项为1，而处于黑色遮蔽区域内的几何遮蔽项为0。

受限于算力，直接计算几何遮蔽项的显式解析式是不可能的。因此，我们需要考虑从一些宏观属性上约束几何遮蔽项。

观察图2，可以看到无论其微表面如何分布，在宏观表面不变的情况下，其投影区域的面积(绿色区域)是不变的。因此，我们可以通过公式(9)约束几何遮蔽。

$$cos\theta_o = \int_M G(w_0,p_m) (w_m \cdot w_o) d p_m(9)$$

其中 为宏观表面法线， 。公式中， 可以被视为各个微表面在方向 上的投影面积 。将其带入到公式(8)中可得公式(10)。

$$L(w_o,M)=\frac{\int_M G(w_o,p_m)(w_m \cdot w_o) L(w_o,p_m)dp_m}{\int_M G(w_o,p_m)(w_m \cdot w_o) dp_m}$$

代入公式(9)可以进一步化简为公式(11)。

$$L(w_o,M)=\frac{\int_M G(w_o,p_m)(w_m \cdot w_o) L(w_o,p_m)dp_m}{cos \theta_o} (11)$$

根据公式(5)所述的几何关系，可得公式(12)。

$$L(w_o, M) = \frac{1}{cos \theta_o} \int_M G(w_o, w_m) (w_m\cdot w_o) L(w_o,w_m) D(w_m)dw_m=\int_M L(w_o, w_m) D_{w_o}(w_m) dw_m (12)$$

其中为了简单记， 囊括了公式(12)所有几何属性，如公式(13)所示。

$$D_{w_o}(w_m) = \frac{1}{cos \theta_o} G(w_o, w_m) (w_m\cdot w_o) D(w_m)(13)$$

有了宏观出射辐射度与微表面出射辐射度之间的关系，只需计算微表面入射辐射度与入射辐射度之间的关系，我们便完成了BRDF推导的最后一块拼图。

定义微表面BRDF函数为公式(14)。

$$\rho(w_i,w_o,w_m) = \frac{dL(w_o,w_m)}{(w_i \cdot w_m)L(w_i) dw_i} (14)$$

根据(13)的定义，可以写出 的另一种形式公式(15)

$$L(w_o, M) = \int dL(w_o, w_m) = \int_{\Omega'} \rho(w_i, w_o, w_m) (w_i \cdot w_m) L(w_i) dw_i(15)$$

接着在公式(12)中，对 关于 微分可得公式(16)。

$$dL(w_o,M) = \int_M dL(w_o, w_m) D_{w_o}(w_m) dw_m=L(w_i)dw_i \int_{\Omega_i} \rho(w_i,w_o,w_m)(w_i\cdot w_m)D_{w_o}(w_m)dw_m (16)$$

与公式(14)类似，定义宏观BRDF函数 如公式(17)所示。

$$\rho(w_i,w_o,M) = \frac{dL(w_o, M)}{cos\theta_i L(w_i)dw_i}(17)$$

其中 为宏观法线与入射光方向的夹角。

将(17)以及(13)带入(16)中可得公式(18)。

$$\rho(w_i,w_o,M) = \frac{1}{cos\theta_i}\int_{\Omega_i} \rho(w_i,w_o,w_m)(w_i\cdot w_m)D_{w_o}(w_m)dw_m$$ $$= \frac{1}{cos \theta_i cos\theta_o}\int_{\Omega_i} \rho(w_i,w_o,w_m)G(w_o, w_m)(w_i\cdot w_m) (w_m\cdot w_o) D(w_m)dw_m$$ $$=\frac{1}{cos \theta_i cos\theta_o}\int_{\Omega_i} \rho(w_i,w_o,w_m)G_2(w_o, w_m, w_i)(w_i\cdot w_m) (w_m\cdot w_o) D(w_m)dw_m(18)$$

终于，经过繁琐的推导，我们得到了微表面BRDF与宏观BRDF之间的关系。这里，需要特别注意的是目前常见的几何遮蔽项一般会被分解为 以及 两个对称的分量，因此一般用 来描述几何遮蔽项。

下面，考虑如何定义微表面的BRDF。对于某块微表面，假设其只发生镜面反射，如公式(19)所示。

$$dL(w_o, w_m)=F(w_h, w_o) L(w_i)\delta_{w_h}(w_m) dw_h (19)$$

其中 为半角向量； 为入射光线； 为菲涅尔项，描述了光线由于折射导致的衰减。公式（19）说明了，入射光线在经过折射后，只有法线方向为 的表面才会反射，因此是标准的镜面反射。

将(19)带入到公式(14)中得公式(20)。

$$\rho(w_i, w_o, w_m) = \frac{dL(w_o,w_m)}{(w_i \cdot w_m)L(w_i) dw_i}=\frac{F(w_h, w_o) L(w_i)\delta_{w_h}(w_m) dw_h}{(w_i \cdot w_m) L(w_i)dw_i}$$ $$= |\frac{dw_h}{dw_i}| \frac{F(w_h, w_o)\delta_{w_h}(w_m)}{(w_i \cdot w_m) }=\frac{F(w_h, w_o) \delta_{w_h}(w_m)}{4(w_i\cdot w_h) (w_i \cdot w_m)} (20)$$

其中关于 的证明将在附录1中展示。

将公式(20)带入到公式(18)中得公式(21)。

$$\rho(w_i,w_o,M) =\frac{1}{cos \theta_i cos\theta_o}\int_{\Omega_i} \rho(w_i,w_o,w_m)G_2(w_o, w_m, w_i) (w_i\cdot w_m) (w_m\cdot w_o) D(w_m)dw_m$$ $$=\frac{1}{cos \theta_i cos\theta_o}\int_{\Omega_i} \frac{F(w_h, w_o) \delta_{w_h}(w_m)}{4(w_i\cdot w_h) (w_i \cdot w_m)} G_2(w_o, w_m, w_i) (w_i\cdot w_m)(w_m\cdot w_o) D(w_m)dw_m$$ $$= \frac{1}{cos \theta_i cos\theta_o} \frac{F(w_h, w_o)}{4(w_i\cdot w_h) (w_i \cdot w_h)} G_2(w_o, w_h, w_i) (w_i\cdot w_h)(w_h\cdot w_o) D(w_h)$$ $$=\frac{F(w_h, w_o)G_2(w_o, w_h, w_i) D(w_h)}{4cos\theta_i cos\theta_o} (21)$$

需要注意的是，在Eric[1]的原文中公式(20)被写为 。个人认为该形式中分母上的 意义不明。而本文采用的形式逻辑上更加清晰且同样能推导出正确结果，故不采用Eric的版本。

可以看到公式(21) 就是Cook-Torrance 模型，而上述计算过程验证了Cook-Torrance模型即为假设所有反射为镜面反射的微表面模型 。

3.法线分布函数

本节将详细讨论微表面模型中 的来龙去脉。关于法线分布，Nathan Reed的博文《Slope Space in BRDF Theory》[2] 有详细描述, 本节将按照该文中的脉络介绍。

在开始前，我们需要重新定义法线分布函数。尽管公式(2) 已经给出了法线分布的定义，然而在实际计算中，讨论具体的微表面如何分布是不切实际的。因此，我们需要更宏观的属性来描述 的性质。

对于单位面积区域 根据公式(3)以及公式(2) 有公式(22)。

$$\int_M (w_g \cdot w_m) D(w_m) dp_m=\int_{\Omega} (w_g \cdot w_m)d w_m = A_M = 1(22)$$

其中 为宏观区域 的面积，既1。在公式(22)中可以看到，法线分布 与微表面微元在 中的投影 的加权求和为单位面积1。这意味着，法线分布不是我们常规认知的定义在微表面法线空间中的概率分布。而是 定义微表面区域在平面xy上的投影中的概率分布。 该性质对下文正确推导法线分布的性质至关重要。

在BRDF理论中，法线分布一般定义在斜率空间(Slope Space)中。Slope Space是一个2D平面空间，其x, y坐标分别对应平面在x方向以及y方向上的斜率 。根据几何关系，平面上的法线可以与斜率空间中的点一一对应，如图3所示。

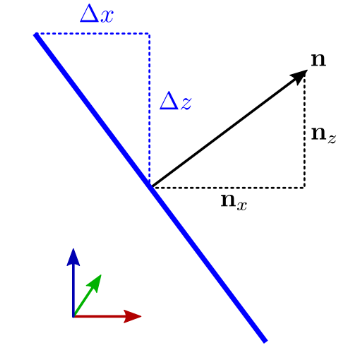
可以看到，图中蓝色三角形与黑色三角形相似，角度相等。因此，物体表面斜率与法线存在如公式(23)的关系。

$$\left\{\begin{matrix} \tilde{x} =\frac{\partial z}{\partial x} = -\frac{n_x}{n_z} \\ \tilde{y}=\frac{\partial z}{\partial y} = -\frac{n_y}{n_z} \end{matrix}\right. (23)$$

其中 为表面斜率空间下的坐标, 为法线在斜率空间下的三个分量。

使用斜率空间定义法线分布有几点好处: 1. 由于微表面模型一般假设微表面的法线分布在上半球上，而斜率空间刚好对应上半球分布，因此定义在该空间下的法线分布不存在越界问题。2. slope space与直角坐标系之间的转化十分简单，计算开销较小。

对于法线分布，一般我们会将其定义成在slope space下的概率分布，接着根据几何关系将其转到直角坐标系下使用。具体来说，对于 , 已知定义在slope space中的法线分布 ,两者需要满足 。因此，计算法线分布的关键在于计算雅可比项 。而Nathan[2] 在文中提到了基于外微分的雅可比项计算方式，下面我们将介绍该方法。

法线方向以及对应slope space坐标在球极坐标系下的表达式如公式(24), (25)所示。

$$\left\{\begin{matrix} x = cos \theta sin \phi \\ y = sin \theta sin \phi \\ z = cos \phi \end{matrix}\right. (24)$$ $$\left\{\begin{matrix} \tilde x = -\frac{x}{z} = - cos \theta tan \phi \\ \tilde y = -\frac{y}{z} = - sin\theta tan \phi \end{matrix}\right. (25)$$

由于 为定义在 平面的概率分布，计算2-form 有公式(26)。

$$dx \wedge dy = (-sin\theta sin\phi d\theta + cos\theta cos\phi d\phi) \wedge (cos\theta sin\phi d\theta +sin\theta cos\phi d\phi)$$ $$= -sin^2\theta sin\phi cos \phi d\theta \wedge d\phi + cos^2\theta sin\phi cos \phi d\phi \wedge d\theta$$ $$= sin\phi cos\phi d\phi \wedge d\theta (26)$$

计算2-form 有公式(27)。

$$d \tilde x \wedge d \tilde y = (sin\theta tan\phi d\theta - cos\theta \frac{1}{cos^2\phi}d\phi) \wedge (-cos\theta tan\phi d\theta - sin\theta \frac{1}{cos^2\phi}d\phi)$$ $$=-sin^2\theta tan\phi \frac{1}{cos^2\phi} d\theta \wedge d\phi + cos^2 \theta tan\phi \frac{1}{cos^2\phi}d\phi$$ $$=tan\phi \frac{1}{cos^2\phi} d\phi \wedge d \theta(27)$$

用公式 (27)除以公式(26) ，可以得到雅可比项如公式(28)所示。

$$\frac{d\tilde x}{dw}=\frac{d \tilde x \wedge d \tilde y}{dx \wedge dy} = \frac{1}{cos^4 \phi} (28)$$

对于任意定义在斜率空间中的概率分布，乘上公式(28)后便可得到对应的直角坐标系下的法线分布。

例如，对于2D高斯分布，乘上公式(28)后有公式(29)。

$$\frac{1}{2 \sigma^2}e^{-\frac{\tilde |x|^2}{2\sigma^2}}\cdot \frac{d\tilde x}{dw}=\frac{1}{2 \sigma^2 cos^4 \theta}e^{-\frac{\tilde |x|^2}{2\sigma^2}}=\frac{1}{acos^4\theta}e^{-\frac{tan\theta^2}{a^2}} (29)$$

可以看到，公式(29)就是Beckmann法线分布，而 为粗糙度。该公式证明了Beckmann法线分布实际是定义在slope space下的正态分布。

另一方面，目前在实践中一般更常用GGX分布。其各项同性形式如公式(30)所示。

$$D(w_m)=\frac{a^2}{\pi ((a^2 - 1)cos^2\theta_m + 1)^2} (30)$$

重新整理该公式得公式(31)。

$$D(w_m) = \frac{a^2}{\pi(a^2cos^2 \theta_m + sin^2\theta_m)^2}$$ $$=\frac{a^2}{\pi cos^4\theta_m(a^2 + tan^2\theta_m)^2}(31)$$

将(31) 中雅可比项 去掉后，可以得到其slope 空间下的形式，如公式(32)所示。

$$D(\tilde x) = \frac{a^2}{\pi (a^2 + |\tilde x|^2)} (32)$$

而公式(32)恰好对应自由度为2的t-分布。该公式验证了GGX法线分布实际是定义在slope space空间下的t-分布。由于GGX分布相比Beckmann分布具有更大的边缘拖尾区域，更能模拟现实现象，因此目前主流的渲染器均采用GGX分布。而t-分布相比正太分布也存在面积更大的拖尾区域。这从侧面也印证了GGX分布就是t-分布的观点。

基于以上讨论，我们可以看到各种千奇百怪的法线分布函数只是经过雅可比变换过后的概率密度函数，它们实际上都是在假定物体表面的法线分布满足某种特殊的概率分布。

4.几何遮蔽项

在法线分布确定后，下面需要做的是确定其空间排布，以计算微表面的几何遮蔽信息。

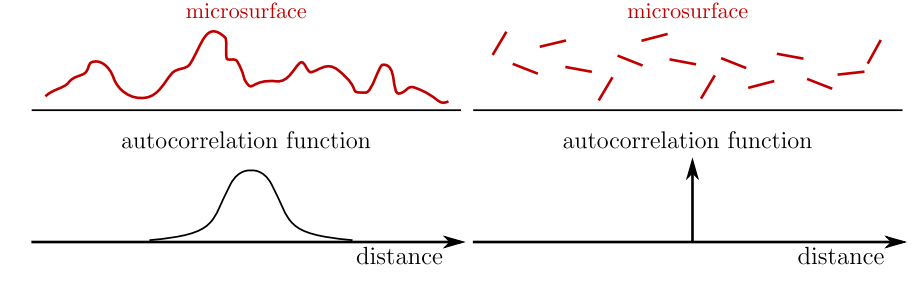
公式(9)展示了几何遮蔽项必须满足的性质，然而这对于唯一确定发现分布，仍远远不够。对于相同的法线分布，如图4所示，其可以存在多种不同的排布方式，而不同的排布方式对应不同的几何遮蔽函数。因此，为了保证系统的唯一解，需要对法线分布做出进一步限制。

目前，工业界最常用的假设是Smith Microsurface Profile，如图4中右边所演示的，该模型假设任意两个微表面之间的高度相互独立，这意味这即使是两个相邻的微表面，其高度依旧可能差距很大。

基于以上假设，其对应的几何遮蔽项可以分为两个部分：1. 由于微表面方向与出射方向大于90，导致的自遮蔽阴影 2. 被远距离未表面遮蔽导致的阴影。两者结合如公式(33)所示。

$$G(w_m, w_o) = G^{local}(w_m,w_o)G^{dist}(w_o)(33)$$

其中， 为第一种自遮蔽阴影情况，其如公式(34)所示，当 时 否则。

$$G^{local}(w_m, w_o) = \chi^{+}(w_m, w_o) (34)$$

将(33), (34)带入到公式(9)中得。

$$cos \theta_o = \int_\Omega G(w_0, p_m) (w_m \cdot w_o) dp_m$$ $$=\int_\Omega G(w_0, w_m)(w_m \cdot w_o) D(w_m)dw_m$$ $$=\int_\Omega G^{local} (w_m, w_o)G^{dist}(w_o)(w_m \cdot w_o) D(w_m) dw_m$$ $$=\int_\Omega \chi^{+}(w_m, w_o) G^{dist}(w_o) (w_m \cdot w_o) D(w_m) dw_m$$ $$= G^{dist}(w_o) \int_\Omega (w_m \cdot w_o) D(w_m) dw_m (35)$$

根据公式(35)， 的定义如公式(36)所示。

$$G^{dist}(w_o) = \frac{cos \theta_o}{ \int_\Omega (w_m \cdot w_o) D(w_m) dw_m } (36)$$

则几何遮蔽函数 的定义如公式(37)所示。

$$G(w_m, w_o)=\chi^{+}(w_m, w_o)\frac{cos \theta_o}{ \int_\Omega (w_m \cdot w_o) D(w_m) dw_m }$$

而在实战过程中，几何遮蔽项一般使用 Smith Masking Function近似，如公式(38)所示。

$$G_{Smith}(w_m, w_o) = \chi^{+}(w_m, w_o) \frac{1}{1 + \Lambda(x)} (38)$$

其中 定义如公式(39)所示。

$$\Lambda(w) = \frac{\sqrt{1 + \frac{(a_xw^l_x)^2 + (a_y w_y^l)^2}{(w^l_z)^2}}-1}{2} (39)$$

其中 为， 在切线空间下第 个坐标轴上的分量， 为各向异性粗糙度。

5. 结语

写这段短文的时候，不禁感概一个看似简单的微表面模型背后竟有如此复杂的数学建模和推导。一方面，该模型面对无穷复杂的现实世界大刀阔斧的简化了大量细节，使材质能简单高效计算的同时与现实材质有较高匹配度。另一方面，如此精巧的模型也只是对有限材质数据集的拟合，并在推导过程中做了大量简化，这对于完全建模真实世界仍存在一定距离。而近年来神经材质的崛起意味着我们可以用复杂的模型准确模拟传统方法难以建模的材质，这可能是突破我们传统建模方式的关键所在。

[1]Eric Heitz.Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs

[2] Nathan Reed. Slope Space in BRDF Theory