再探体渲染(一)-- 理论
由于之前实习接触到体积雾相关的东西,想顺带把这一系列相关渲染技术复现一下,于是从这篇文章开始看起RayMarching实时体积云渲染入门(上) - 知乎 [1] 。实现到一半发现自己很多理论不扎实的地方(代码和公式没法联系到一起),遂重新研读了PBRT的Volume Rendering [2]部分。不得不说,这东西不隔一阵子梳理一下真的巨容易忘,也应了闫在课上说的”常看常新“了。
微分形式
以下部分均来自[2]
对于一小段体积微元的出射强度
吸收
当入射光线
其中,
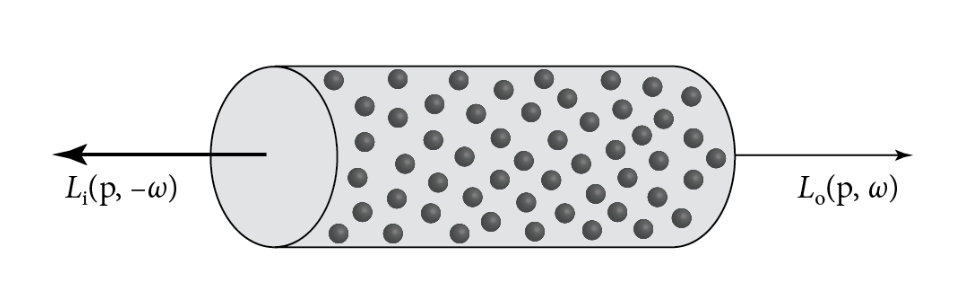
自发光
由于光线穿过的微元内粒子的化学,辐射等现象导致的能量出射。其微分形式和吸收类似
其中
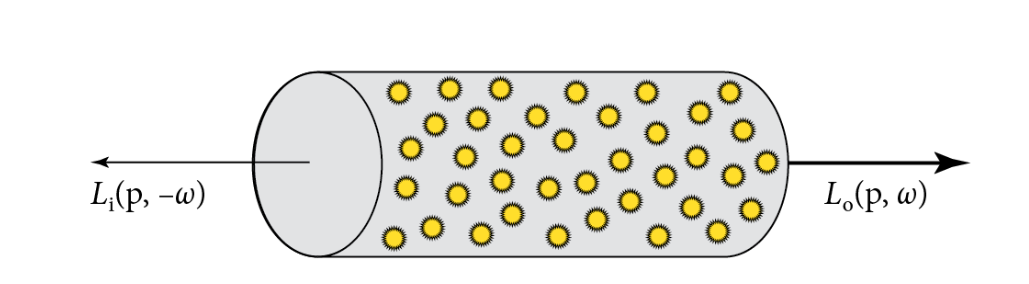
出射/入射
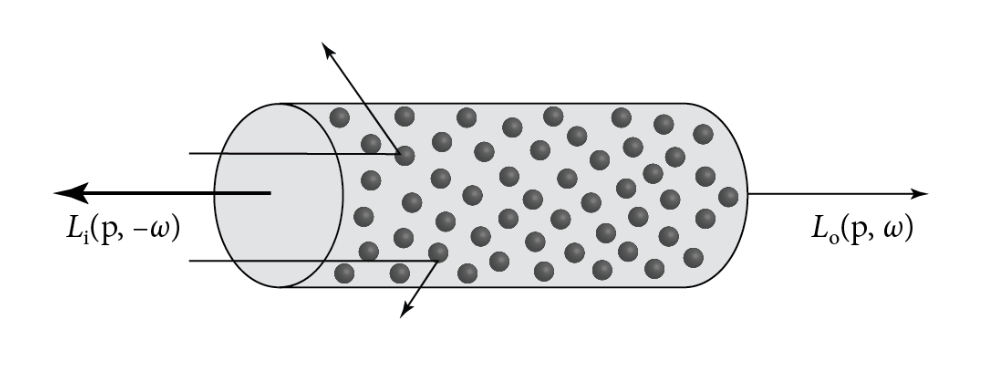
描述了由于光线在粒子之间不断反射的现象。出射描述了由于本该输出的光线反射到其它方向造成的损失(吸收是光线进入到粒子内部 造成的损失,而出射是粒子之间 反射现象造成的损失)。其公式为:
其中
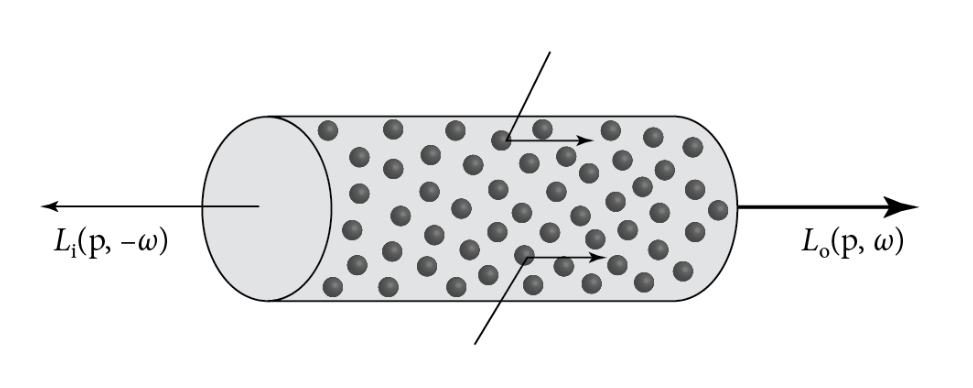
与出射相对应,入射描述了部分“幸运”光线反射到出射方向上从而额外增加的能量。其公式为:
其中
入射能量项可以说是实时体积雾渲染最重要的一项。很多有趣的效果(天空体积云,上帝光,手电筒光的丁达尔效应)均来自此项。
合并形式
前文中介绍的诸多现象可以简单分为两类,减少能量(吸收/出射), 增加能量(入射/自发光)。而将这两种效应相加便可得到整个体渲染方程的微分形式。
其中,方程加号左边边对应能量衰减项,加号右边对应能量增加项。其中
积分形式— Volume Render Equation
transmittance
对于体积雾中的散射/吸收现象,其满足微分方程:
定义边界条件:光线起始于位置
由于
则光线穿过体积介质从
由于
这个性质在使用ray marching的求解器中十分常用。可以将整个光线的transmittance拆分成每一小步的transmittance的乘积。
而Tr项的指数部分被称为光学密度(Optical Thickness),其公式为:
当体积雾的密度为常数时,(2.3)可以写成:
其与Beer’s law 对应。
Volume Render Equation
无论是实时渲染还是离线光追,一般都使用积分形式。因此,从(1.6)推导体渲染方程的积分形式是必不可少的。计算过程主要参考[3]
方程的边界条件为: 沿着
下面推导公式(1.6)的积分形式。由于微分方程不可拆分(对
注意到(1.6)是一阶非齐次线性微分方程 , 该方程存在解析通解。
为表示简便,令
将
由于
注意,这里
观察得,(2.7)满足一阶非齐次线性微分方程
令
则
带入(2.7)中得:
代入边界条件,对两边在0~d的范围内积分得:
其中
现在我们使用
这便是我们在PBRT中看到的经典渲染方程的形式。
这个结论还是很优雅的。简洁,且每一项都有明确的物理意义。如下图所示,每个点输入的辐射度等于其它表面反射并穿体积雾衰减后的辐射度(对应
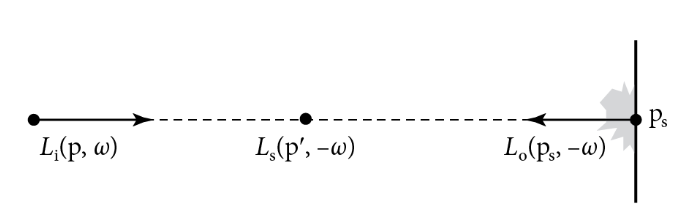
null scattering
这部分和实时渲染没什么关系,只是对PBRT 关于 null scattering公式的补充说明。PBRT中没有给出null scattering相关公式的推导,这里主要参考了[4]
TODO.
Phase Function
Phase Function的物理意义是光线从
最后简单介绍一下PBRT中出现的Phase Function[2]。
各项同性象函数
各项异性象函数
其中
[1] https://zhuanlan.zhihu.com/p/248406797
[2] https://pbr-book.org/4ed/Volume_Scattering
[4] https://cs.dartmouth.edu/~wjarosz/publications/miller19null.pdf





