本文为The Material Point Method for Simulating Continuum Materials 的笔记。首先本文介绍了push forward和pull back,它们为欧拉视角和拉格朗日视角之间的转换提供了重要视角。接着,本文从形变梯度,拉格朗日欧拉视角,压力的定义出发,根据动量守恒以及能量守恒推导了整个系统应遵守的核心方程。物质质点法采用了欧拉以及拉格朗日的混合视角,对空间给出了质点以及网格两种不同离散形式,本文还讨论了这两种离散形式之间物理量如何转化,以及核心方程的离散化形式。最后,本文给出了一个简单原始的mpm实现,并详细解读它的代码。
Push Forward and Pull Back 对于一个双射映射,能找到
对于任意映射
Push Forward和Pull back在拉格朗日视角和欧拉视角之间相互转换起着重要作用。它定义了如何看待两个变化着的系统的不变量。
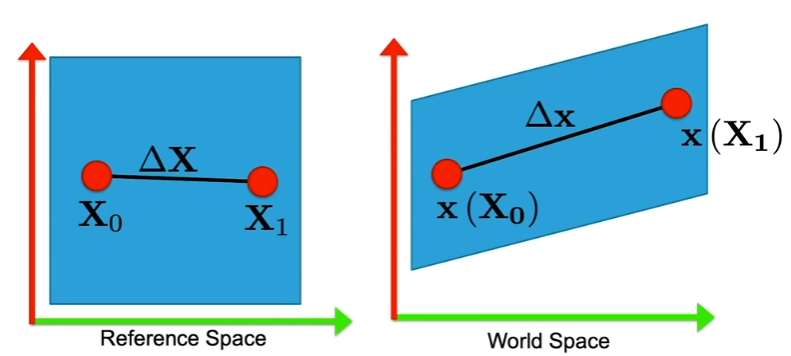
形变梯度 为了研究物体随时间形变的受力,我们通常会研究物体的deform空间以及reference空间。其中reference空间种物体处于不受任何力的自然的状态
形变梯度定义了一个体积微元经过t时刻后发生了哪些线性变换,如图所示
其中在deform 空间下
我们定义
欧拉视角和拉格朗日视角 在拉格朗日视角下,系统的速度和加速度可以定义为:
而欧拉视角为拉格朗日视角的push forward:
将(2)带入(1)中可得:
令
对于更一般的函数
若f为形变梯度F(
则:
积分变换 对于线微元
对该微元施加任意形变
则该体微分变为(
对于形变后的区域和形变前的区域
其中
对于法线方向为
令
则定义在
压力场 压力可以定义为一个在
其中
柯西压力场的定义可以从该定义中衍生(柯西压力为Piola-Kirchoff由
由于在刚性变化下(
在刚体变换中
在图形中,一般常常把
其中
一种常用的模型为Neo-Hookean模型,该模型的形式为:
其Piola-Kirchoff可被定义为
另一种常用的模型fixed corotated model为:
其Piola-Kirchoff张量可以被定义为
其中
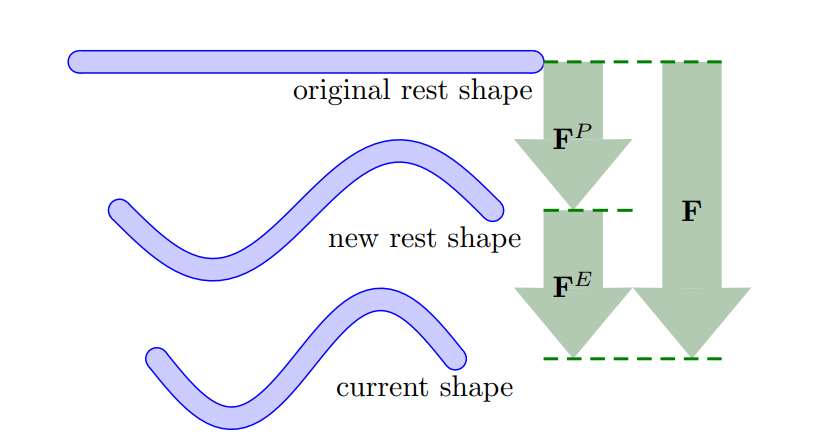
塑性形变 对于形变梯度
在计算压力过程中,只有
对于雪的塑性形变的模拟,一种常见的方式是将
对于模拟的第
在
接着我们通过奇异值分解,将
最后,通过
雪材质的一大特点为挤压时受力更大,这可以被建模为受到挤压时,其
动量守恒,质量守恒 在拉格朗日视角下,令速度
其中
对于欧拉视角下的动量守恒可以将11改为
其中对于
对于
由于伴随矩阵的元素
则
带入(13)中有:
则将(14)带入(12)中有:
将
对于动量守恒,对于物体内部的受力场
则动量守恒有:
对于方程的左边:
由于质量守恒
对于方程右边:
将方程左边全部push forward得到该方程在欧拉视角下的形式
同样的,可以对方程的左边做pull back:
由于
将16带入方程得:
方程的弱解 对于拉格朗日视角下的动量守恒方程(17),忽略外力项
对点乘任意函数
对于欧拉视角的方程假设
又由于公式(6):
则公式(18)在欧拉视角下的形式是:
这里
物质点 在MPM中,会在计算advection时将物质表示为物质点,在拉格朗日视角下模拟。而在计算物质点之间的压力场时,则会将物质点投影到欧拉网格上,在欧拉视角下求解。物质点到网格的来回投影需要差值函数,一般的,cubic样条和Quadratic样条都是比较常用的函数
而对每个物质点
对于系统中的每个物质点,可以定义其质量为
则可以定义由拉格朗日视角下物质点的质量/动量转移到欧拉网格下的公式:
根据动量以及质量转移,可以推得各个网格的速度:
从网格到质点的转移类似,由于在模拟时一般假设质点的质量不变,因此只需要转移其速度
时间离散化 将(19)时间离散化有:
这里
这里将下标表示中的
需要注意的是
空间离散化 将
其中
这里i,j等下标的求和符号均被省略
令
原式左手:
由于该式对任意
则原式等于
者可以视作对
由于
将(27)带入(26)中可得
对于每个质点
将其带入(28)中得到:
对于粒子
而对于
其中
另一种方法则为将整个积分域由
将公式(6)以及(31)带入(29)减号右边得到:
将上式带入(28)中得:
计算形变梯度 直接计算形变梯度在mpm里是十分困难的,但是可以通过时间离散化后更新其值来估计。根据公式(2.1)有:
对于
对
将上式带入(32)得:
潜在能量和受力 假设欧拉网格点的位置会随着时间运动(TODO 定义
对于系统的潜在能量函数可以被定义为:
根据拉格朗日方程,我们可以通过对潜在能函数求广义坐标的导数分析系统受力。(动机)
对其某个粒子的位置
(TODO)其速度可以表达为
对
将(35)带入(34)有:
对比(36)和(31)减号后半部分,不难发现:
其中
显式前向欧拉 APIC 相比传统的PIC,APIC对从粒子到网格动量的transfer过程做了部分改动。
关于(e.2)公式的详细说明可以见论文笔记 The Affine Particle-In-Cell Method(TODO)
其中
其中
更新形变梯度 根据公式(33)可得每个粒子的形变梯度
计算受力 根据公式(36)可以计算各个欧拉网格在不同时间点的受力公式:
完整步骤 整个过程分为以下几步:
从粒子通过(e.1),(e.2)transfer到欧拉网格
计算网格速度
(可选)标记质量非0的网格,在后续的模拟中只考虑这些网格。
根据公式(e.4), 计算网格受力
更新网格速度
更新网格形变梯度根据公式(e.3)
将网格速度重新投影回各个粒子上
代码解读 一个navie版本的基于前向欧拉的mpm实现如下所示 (数据声明以及场景设定的代码来自99行冰雪奇缘 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 import taichi as tiimport numpy as npti.init(arch=ti.gpu) quality = 1 n_particles, n_grid = 6000 * quality ** 2 , 128 * quality dx, inv_dx = 1 / n_grid, float (n_grid) drt = 2e-3 dt = 1e-4 / quality p_vol, p_rho = (dx * 0.5 )**2 , 1 p_mass = p_vol * p_rho E, nu = 0.1e4 , 0.2 mu_0, lambda_0 = E / (2 * (1 + nu)), E * nu / ((1 +nu) * (1 - 2 * nu)) x = ti.Vector.field(2 , dtype=float , shape=n_particles) v = ti.Vector.field(2 , dtype=float , shape=n_particles) F = ti.Matrix.field(2 , 2 , dtype=float , shape=n_particles) material = ti.field(dtype=int , shape=n_particles) grid_v = ti.Vector.field(2 , dtype=float , shape=(n_grid, n_grid)) grid_m = ti.field(dtype=float , shape=(n_grid, n_grid)) grid_f = ti.Vector.field(2 , dtype=float , shape=(n_grid, n_grid)) g = ti.Vector([0 , -50 ]) h = 0.3 @ti.func def get_grid_idx (idx, i, j ): res = idx + ti.Vector([i, j]) return ti.math.clamp(res, 0 , n_grid) @ti.kernel def p2g (): for i,j in grid_v: grid_v[i, j] = ti.Vector([0 , 0 ]) grid_m[i, j] = 0 grid_f[i, j] = ti.Vector([0 , 0 ]) for p in range (n_particles): x_p = x[p] v_p = v[p] F_p = F[p] U, sig, V = ti.svd(F_p) J = 1.0 for d in range (2 ): J *= sig[d, d] mu, la = h * mu_0, lambda_0 * h PFTV = (2 * mu * (F_p - U @ V.transpose()) @ F_p.transpose() + la * (J - 1 ) * J) * p_vol x_i_m_1 = (x_p * inv_dx + 0.5 ).cast(int ) - 1 fx = x_p * inv_dx - x_i_m_1.cast(float ) w = [0.5 * (1.5 - fx) ** 2 , 0.75 - (fx - 1 ) ** 2 , 0.5 * (fx - 0.5 ) ** 2 ] dw = [(fx - 1.5 ) * inv_dx, (2.0 - 2.0 * fx) * inv_dx, (fx - 0.5 ) * inv_dx] for i,j in ti.static(ti.ndrange(3 , 3 )): w_ij = w[i][0 ] * w[j][1 ] grid_idx = get_grid_idx(x_i_m_1, i, j) grid_m[grid_idx] += p_mass * w_ij grid_v[grid_idx] += p_mass * v_p * w_ij grid_f[grid_idx] += - PFTV @ ti.Vector([ dw[i][0 ] * w[j][1 ], w[i][0 ] * dw[j][1 ]]) @ti.kernel def g2p (): for i, j in grid_v: if grid_m[i, j] == 0 : grid_v[i, j] = 0 else : grid_v[i, j] = grid_v[i, j] / grid_m[i, j] grid_v[i, j] += (g + grid_f[i, j] / grid_m[i, j]) * dt if i == n_grid - 1 : grid_v[i, j][0 ] = min (grid_v[i, j][0 ], 0 ) elif i == 0 : grid_v[i, j][0 ] = max (grid_v[i, j][0 ], 0 ) elif j == n_grid - 1 : grid_v[i, j][1 ] = min (grid_v[i, j][1 ], 0 ) elif j == 0 : grid_v[i, j][1 ] = max (grid_v[i, j][1 ], 0 ) grid_v[i, j][0 ] *= 0.8 for p in range (n_particles): x_p = x[p] x_i_m_1 = (x_p * inv_dx + 0.5 ).cast(int ) - 1 fx = x_p * inv_dx - x_i_m_1.cast(float ) w = [0.5 * (1.5 - fx) ** 2 , 0.75 - (fx - 1 ) ** 2 , 0.5 * (fx - 0.5 ) ** 2 ] dw = [(fx - 1.5 ) * inv_dx, (2.0 - 2.0 * fx) * inv_dx, (fx - 0.5 ) * inv_dx] F_p = F[p] new_F_p = F_p new_v_p = ti.Vector([0 , 0 ], dt=float ) for i,j in ti.static(ti.ndrange(3 , 3 )): grad_w_ip = ti.Vector([ dw[i][0 ] * w[j][1 ], w[i][0 ] * dw[j][1 ]]) w_ip = w[i][0 ] * w[j][1 ] grid_idx = get_grid_idx(x_i_m_1, i, j) v_i = grid_v[grid_idx] new_F_p += dt * v_i.outer_product(grad_w_ip) @ F_p new_v_p += w_ip * v_i F[p] = new_F_p v[p] = new_v_p x[p] += new_v_p * dt group_size = n_particles // 2 @ti.kernel def initialize (): for i in range (n_particles): x[i] = [ti.random() * 0.2 + 0.3 + 0.10 * (i // group_size), ti.random() * 0.2 + 0.05 + 0.32 * (i // group_size)] material[i] = i // group_size v[i] = ti.Matrix([0 , 0 ]) F[i] = ti.Matrix([[1 , 0 ], [0 , 1 ]]) initialize() gui = ti.GUI("navie mpm" , res=512 , background_color=0x112F41 ) while not gui.get_event(ti.GUI.ESCAPE, ti.GUI.EXIT): for s in range (int (drt // dt)): p2g() g2p() colors = np.array([0xEEEEF0 , 0xED553B , 0xEEEEF0 ], dtype=np.uint32) gui.circles(x.to_numpy(), radius=1.5 , color=colors[material.to_numpy()]) gui.show()
接下来本文将解读模拟的主体部分。
每个模拟步骤分为初始化,粒子到网格,网格更新,网格到粒子4个部分。
在初始化阶段,需要把网格的质量,速度,力等属性清0
1 2 3 4 for i,j in grid_v: grid_v[i, j] = ti.Vector([0 , 0 ]) grid_m[i, j] = 0 grid_f[i, j] = ti.Vector([0 , 0 ])
接着在粒子到网格阶段,我们首先需要根据公式(e.4)计算各个粒子对应的力
1 2 3 4 5 6 7 8 9 10 11 12 13 ... for p in range (n_particles): x_p = x[p] v_p = v[p] F_p = F[p] U, sig, V = ti.svd(F_p) J = 1.0 for d in range (2 ): J *= sig[d, d] mu, la = h * mu_0, lambda_0 * h PFTV = (2 * mu * (F_p - U @ V.transpose()) @ F_p.transpose() + la * (J - 1 ) * J) * p_vol
其中PFTV 为(e.4)中的
接着,根据公式(e.1)以及(e.4) (由于目前我们的实现不是APIC因此动量的转换只是简单的
我们将粒子的受力,质量以及动量转移到网格上
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 ... x_i_m_1 = (x_p * inv_dx + 0.5 ).cast(int ) - 1 fx = x_p * inv_dx - x_i_m_1.cast(float ) w = [0.5 * (1.5 - fx) ** 2 , 0.75 - (fx - 1 ) ** 2 , 0.5 * (fx - 0.5 ) ** 2 ] dw = [(fx - 1.5 ) * inv_dx, (2.0 - 2.0 * fx) * inv_dx, (fx - 0.5 ) * inv_dx] for i,j in ti.static(ti.ndrange(3 , 3 )): w_ij = w[i][0 ] * w[j][1 ] grid_idx = get_grid_idx(x_i_m_1, i, j) grid_m[grid_idx] += p_mass * w_ij grid_v[grid_idx] += p_mass * v_p * w_ij grid_f[grid_idx] += - PFTV @ ti.Vector([ dw[i][0 ] * w[j][1 ], w[i][0 ] * dw[j][1 ]])
其中,关于权重的计算,这里我们用了和99行冰雪奇缘 类似的小trick。
在transfer过程中,一个粒子需要搜索其
令
而对于第
于是,便有
1 2 3 4 5 6 7 x_i_m_1 = (x_p * inv_dx + 0.5 ).cast(int ) - 1 fx = x_p * inv_dx - x_i_m_1.cast(float ) w = [0.5 * (1.5 - fx) ** 2 , 0.75 - (fx - 1 ) ** 2 , 0.5 * (fx - 0.5 ) ** 2 ] ... for i,j in ti.static(ti.ndrange(3 , 3 )): w_ij = w[i][0 ] * w[j][1 ]
对于
令
则对于第
这对应着代码
1 2 3 4 5 dw = [(fx - 1.5 ) * inv_dx, (2.0 - 2.0 * fx) * inv_dx, (fx - 0.5 ) * inv_dx] for i,j in ti.static(ti.ndrange(3 , 3 )): ... grid_f[grid_idx] += - PFTV @ ti.Vector([ dw[i][0 ] * w[j][1 ], w[i][0 ] * dw[j][1 ]])
结束从粒子到网格后,在网格更新阶段。我们会根据之前的网格力和速度的计算结果更新网格的速度。其中对于处于边界的网格,我们会额外计算边界条件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 for i, j in grid_v: if grid_m[i, j] == 0 : grid_v[i, j] = 0 else : grid_v[i, j] = grid_v[i, j] / grid_m[i, j] grid_v[i, j] += (g + grid_f[i, j] / grid_m[i, j]) * dt if i == n_grid - 1 : grid_v[i, j][0 ] = min (grid_v[i, j][0 ], 0 ) elif i == 0 : grid_v[i, j][0 ] = max (grid_v[i, j][0 ], 0 ) elif j == n_grid - 1 : grid_v[i, j][1 ] = min (grid_v[i, j][1 ], 0 ) elif j == 0 : grid_v[i, j][1 ] = max (grid_v[i, j][1 ], 0 ) grid_v[i, j][0 ] *= 0.8
注意在这步之前grid_v 中存储的是各个网格的动量,而在这步之后,grid_v 存储的是网格真正的速度。
对于质量为0的网格,为了避免除0错误,需手动将其速度设为0。而对于质量极小的网格,由于在后续的计算中其极大的速度会被权重系数
最后在网格到粒子阶段,会把各个网格的速度重新映射回粒子。这里权重及其梯度的算法和前文一致,不再赘述。最后根据公式(e.3),(e.5),(e.6)更新粒子的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 for p in range (n_particles): x_p = x[p] x_i_m_1 = (x_p * inv_dx + 0.5 ).cast(int ) - 1 fx = x_p * inv_dx - x_i_m_1.cast(float ) w = [0.5 * (1.5 - fx) ** 2 , 0.75 - (fx - 1 ) ** 2 , 0.5 * (fx - 0.5 ) ** 2 ] dw = [(fx - 1.5 ) * inv_dx, (2.0 - 2.0 * fx) * inv_dx, (fx - 0.5 ) * inv_dx] F_p = F[p] new_F_p = F_p new_v_p = ti.Vector([0 , 0 ], dt=float ) for i,j in ti.static(ti.ndrange(3 , 3 )): grad_w_ip = ti.Vector([ dw[i][0 ] * w[j][1 ], w[i][0 ] * dw[j][1 ]]) w_ip = w[i][0 ] * w[j][1 ] grid_idx = get_grid_idx(x_i_m_1, i, j) v_i = grid_v[grid_idx] new_F_p += dt * v_i.outer_product(grad_w_ip) @ F_p new_v_p += w_ip * v_i F[p] = new_F_p v[p] = new_v_p x[p] += new_v_p * dt
代码的运行结果如图所示: