CS417 physics based animation笔记

本文为课程CS417 Physics based animation的课程笔记。本课程从欧拉拉格朗日方程以及数值算法出发，介绍了如何模拟弹簧质点系统，有限元，刚体模拟以及流体模拟（流体还没做，摆烂）。对于课程内的公式，本文在力所能及的范围内适当补充了推导过程。

1.Euler-Lagrange

任何力学系统应满足的法则，给出广义坐标时能快速对系统受力分析。

两点之间直线最短:

对力学系统，定义广义坐标 ,广义速度 ,能量函数 ,动能函数 ,势能函数 ，有:

$$\begin{matrix} L=T-V (1.1) \\ S(q,\dot{q})=\int_{t_0}^{t_1} L(q,\dot{q})dt \end{matrix}$$

当物体运动的起始点和结束点 给定时，泛函 取得最小时系统稳定。当 稳定时，其偏导数趋近于0:

$$S(q,\dot{q})=S(q + \delta q,\dot{q} + \delta \dot{q}) (1.2)$$ $$S(q + \delta q,\dot{q} + \delta \dot{q})$$ $$=\int_{t_0}^{t_1} L(q+\delta q,\dot{q} + \delta \dot{q}) dt$$ $$=\int_{t_0}^{t_1} L(q,\dot q) dt + \int_{t_0}^{t_1} \frac{\partial L}{\partial q} \delta q + \frac{\partial L}{\partial \dot q}\delta \dot q dt$$ $$带入 (1.2) : \int_{t_0}^{t_1} \frac{\partial L}{\partial q} \delta q + \frac{\partial L}{\partial \dot q}\delta \dot q dt = 0$$ $$对后半部分分部积分:\int_{t_0}^{t_1} \frac{\partial L}{\partial q} \delta q dt - \int_{t_0}^{t_1}\frac{d}{dt} \frac{\partial L}{\partial \dot q}\delta qdt + \frac{\partial L}{\partial \dot q} \delta q |_{t_0}^{t_1} = 0$$ $$由于q在t_0,t_1时刻为定点q_0,q_1:\frac{\partial L}{\partial \dot q} \delta q |_{t_0} ^{t_1} = 0$$ $$则:\int_{t_0} ^{t_1} (\frac{\partial L}{\partial q} - \frac{d}{dt} \frac{\partial L}{\partial \dot q} )\delta q dt = 0$$ $$由于\delta q 任意:\frac{\partial L}{\partial q} = \frac{d}{dt} \frac{\partial L}{\partial \dot q}(1.3)$$

(1.3)便是Euler-Lagrange方程。对于任意力学系统，均需满足该方程。当 时，称 为系统广义力。

下面，我们在一维弹簧质点系统验证欧拉拉格朗日方程的正确性:

为位置， 为速度， 为质点动能， 为弹簧势能。

$$q = x,v = \dot q, T=\frac{1}{2} mv^2,V= \frac{1}{2}kx^2,L=T-V=\frac{1}{2}(mv^2-kx^2)$$ $$\frac{\partial L}{\partial q} =-kx,\frac{\partial L}{\partial \dot q} = mv$$ $$带入(1.3) m\frac{d}{dt} v=-kx (1.4)$$

而(1.4) 为牛顿第二定律对应的胡克定律方程。

2.Numeric Method

一般来说动力学系统涉及2阶微分方程 将 打包为一个向量 我们可以将微分方程转为一阶的微分方程: ，对于该方程我们有几种数值解法

2.1 Forward Euler:

将 一阶泰勒展开:

$$A\frac{1}{\Delta t} (y^{t+1}- y^t)=f(y)$$ $$y^{t+1}=y^t + \Delta t A^{-1}f(y^t) (2.1)$$

2.2Runge-Kutta

$$y^{t+1}=y^t+\Delta t A^{-1} (\alpha f(y^{t+a}) + \beta f(y^{t + b})) (2.2)$$

当 时，退化为Forward Euler

当 时，退化为 Heun’s Method:

$$y^{t+1}= y^t + \frac{\Delta t}{2} A^{-1} (f(y^t) + f(\hat y ^{t + 1})$$ $$\hat y ^{t + 1} = y^t + \Delta t A^{-1} f(y^t) (2.3)$$

最为常用的Runge-Kutta方法为:

$$k_1 = A^{-1}f(y^t)$$ $$k_2 = A^{-1}f(y^t + \frac{\Delta t}{2} \cdot k_1)$$ $$k_3=A^{-1}f(y^t + \frac{\Delta t}{2} \cdot k_2)$$ $$k_4 = A^{-1} f(y^t + \Delta t \cdot k_3)$$ $$y^{n+1} = y^t+\frac{ \Delta t}{6} A^{-1} (k_1 + 2k_2 + 2k_3 + k_4) (2.4)$$

2.3 Backward Euler:

当函数 是线性变换时，我们可以利用这点推导出逆向Euler公式：

$$A\frac{1}{\Delta t} (y^{t + 1} - y^{t}) = By^{t+1}$$ $$(I-A^{-1}B\Delta t)y^{t+1} = y^{t}$$ $$y^{t+1} = (I-A^{-1}B\Delta t)^{-1} y^{t}$$

Backward Euler的优点之一是，它会让系统整体能量不断减少。

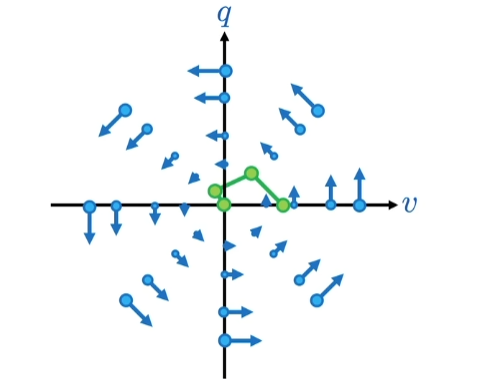
从Phase Space可以看到，每一步迭代 的坐标都落到轨迹圆的内部，一直迭代下去直到系统静止。这种现象让模拟器数值十分稳定(不会让物体速度越来越快)，而且有助于模拟阻力。

2.4 Sycmplectic Euler:

结合了Forward Euler和Backward Euler的优点和缺点。它能保证系统整体的能量不会随着时间变化而太大的变化。

它的做法十分简单，用Forward Euler更新一步，再由Backward Euler更新一步。例如:在弹簧质点系统中，用Forward Euler更新速度，接着，用Backward Euler更新位置:

$$v^{t+1}=v^t-\frac{k}{m}q^t$$ $$q^{t+1}=q^t+\Delta t v^{t+1}$$

3.Mass-Spring System 3D

3.1 双质点单弹簧

假设第一个质点坐标维 第二个为,系统广义坐标为 ,弹簧劲度系数为，质点质量矩阵为 ,弹簧初始长度为则弹簧的潜在能为:

$$V_k= \frac{1}{2} k(|q_0-q_1|-l_0)^2=\frac{1}{2}k(\sqrt{q^TB^TBq}-l_0)^2(3.1)$$

其中( 也成立，且不会对公式推导产生影响)

由广义力

$$\frac{\partial V}{\partial q} = k(\sqrt{q^TB^TBq} - l_0) \cdot \frac{1}{2\sqrt{q^TB^TBq}} \cdot 2 B^TBq= k B^TBq(1 - \frac{l_0}{\sqrt{q^TB^TBq}}) (3.2)$$

在积分时使用backward euler算法:

$$M\dot{q}^{t+1} = M\dot{q}^t + \Delta tf(q^{t+1}) (3.3)$$ $$q^{t+1}= q^{t} + \Delta t \dot{q}^{t+1} (3.4)$$

由于 非线性函数，使用Linearly-Implicit euler 近似，将(3.4)代入(3.3)得:

$$M\dot{q} ^{t +1}= M\dot q^t + \Delta t f(q^t + \Delta t \dot{q} ^ {t+1})$$ $$(对f一阶taylor展开) M\dot{q}^{t + 1}=M\dot{q}^t + \Delta t f(q^t) + \Delta t^2 (\frac{\partial f(q^t)}{\partial q})\dot{q}^{t+1}$$ $$(M-\Delta t^2 (\frac{\partial f(q^t)}{\partial q}))\dot{q}^{t+1}=M\dot{q}^t+\Delta t f(q^t) (3.5)$$

求解线性系统(3.5)就可得到 ,公式去掉 项便退化为forward euler。

求解时涉及

关于 :

$$\frac{\partial V}{\partial q} = kB^TBq-kl_0\frac{B^TBq}{\sqrt{q^TB^TBq}}$$ $$\frac{\partial kB^TBq}{\partial q}= kB^TB$$ $$\frac{\partial \frac{kl_0B^TBq}{\sqrt{q^TB^TBq}}}{\partial q}= (B^TBq)\frac{\partial \frac{1}{\sqrt{q^TB^TBq}}}{\partial q} kl_0 + kl_0 \frac{1}{\sqrt{q^TB^TBq}} \frac{\partial B^TBq}{\partial q}$$ $$=-B^TBq\cdot(\frac{1}{2} \frac{2q^TB^TB}{(\sqrt{q^TB^TBq})^3} kl_0)+kl_0\frac{B^TB}{\sqrt{q^TB^TBq}}$$ $$\frac{\partial V^2}{\partial q^2}=kB^TB(1 - \frac{l_0}{\sqrt{q^TB^TBq}} + \frac{l_0qq^T B^TB}{(\sqrt{q^TB^TBq}) ^3} ) (3.6)$$

由于 对称,

有上述结论，我们建立了求解单弹簧质点系统的所有数学工具。

3.2 多质点系统

多质点系统可通过分解为多个双质点系统求解。

令 , ，若第个弹簧连接 两点,则,潜在能可以写为:

$$V=\sum_i^n \frac{1}{2}k(\sqrt{q_i^TB^TBq_i}-l_0)^2=\frac{1}{2}k\sum_i^n V_k(q_i)=\frac{1}{2}k\sum_i^nV_k(S_iq)(3.7)$$

其中

$$S_iq=q_i,S_i\in R^{6\times 3n} S_i=\begin{pmatrix} 0 &... &I_i &0 \\ 0 & I_k & ... &0 \end{pmatrix}(I_i在S第3i列,I_k在S第3k列)(3.8)$$

对广义力公式也就有

$$f=-\frac{\partial V}{\partial q}=-\frac{1}{2} k \sum_i^nS_i^T\frac{\partial V_k(q_i)}{\partial q_i}(3.9)$$ $$\frac{\partial f}{\partial q}=-\frac{\partial ^2 V}{\partial q^2}=-\frac{1}{2}k\sum_i^n (S^T_i \frac{\partial^2 V_k(q_i)}{\partial q_i^2})(S_i^T)^T=-\frac{1}{2}k\sum_i^n S^T_i \frac{\partial^2 V_k(q_i)}{\partial q_i^2}S_i (3.10)$$

通过些公式，公式(3.5) 可扩展到高维。在每次迭代中，找出所有弹簧单个计算 和 乘上矩阵 后将其叠加起来，带入(3.5)中求解线性系统，便可求解。计算 和 的代码为。

void assemble_forces(Eigen::VectorXd &f, Eigen::Ref<const Eigen::VectorXd> q, Eigen::Ref<const Eigen::VectorXd> qdot, 
                     Eigen::Ref<const Eigen::MatrixXd> V, Eigen::Ref<const Eigen::MatrixXi> E, Eigen::Ref<const Eigen::VectorXd> l0s, 
                     double mass, double k) 
{ 
	//assemble force vector

    f.resize(V.rows() * 3);
    f.setZero();


    //apply spring forces
    for (uint32_t i = 0;i < E.rows();i++)
    {
        uint32_t v0 = E(i, 0), v1 = E(i, 1);
        Eigen::Vector3d q0(q(v0 * 3), q(v0 * 3 + 1), q(v0 * 3 + 2));
		Eigen::Vector3d q1(q(v1 * 3), q(v1 * 3 + 1), q(v1 * 3 + 2));


        double l0 = l0s(i);
        Eigen::Vector6d spring_force;
        dV_spring_particle_particle_dq(spring_force, q0, q1, l0, k);
        spring_force = -spring_force;

        f(3 * v0) += spring_force(0);
        f(3 * v0 + 1) += spring_force(1);
        f(3 * v0 + 2) += spring_force(2);
        f(3 * v1) += spring_force(3);
        f(3 * v1 + 1) += spring_force(4);
        f(3 * v1 + 2) += spring_force(5);
    }
};

void assemble_stiffness(Eigen::SparseMatrixd &K, Eigen::Ref<const Eigen::VectorXd> q, Eigen::Ref<const Eigen::VectorXd> qdot, 
                     Eigen::Ref<const Eigen::MatrixXd> V, Eigen::Ref<const Eigen::MatrixXi> E, Eigen::Ref<const Eigen::VectorXd> l0, 
                     double k) 
{ 
    K.resize(V.rows() * 3, V.rows() * 3);
	K.setZero();
	triplets.clear();
    accumlatedTriplets.clear();

    {
		//triplets.clear();
        Timer timer("compute stiffness per-spring");
		for (uint32_t i = 0; i < E.rows(); i++)
		{
			uint32_t v0 = E(i, 0), v1 = E(i, 1);
			Eigen::Vector3d q0(q(v0 * 3), q(v0 * 3 + 1), q(v0 * 3 + 2));
			Eigen::Vector3d q1(q(v1 * 3), q(v1 * 3 + 1), q(v1 * 3 + 2));
			double l = l0(i);

			Eigen::Matrix66d H;
			d2V_spring_particle_particle_dq2(H, q0, q1, l, k);
			H = -H;


			SetK(v0, v1, triplets, H);
		}
    }
	
    {
        Timer timer("sort triplets");
		std::sort(triplets.begin(), triplets.end(), [&](const Tri& lhs, const Tri& rhs)
			{
				if (lhs.row() < rhs.row())
				{
					return true;
				}
				else if (lhs.row() > rhs.row())
				{
					return false;
				}
		return lhs.col() < rhs.col();
			}
		);
		//trick: insert a dummy triplet
		triplets.push_back(Tri(V.rows() * 3 + 1, V.rows() * 3 + 1, 0));
    }
    

    {
        Timer timer("accumulation");
		uint32_t row = triplets[0].row(), col = triplets[0].col();
		double val = triplets[0].value();
		for (uint32_t i = 1; i < triplets.size(); i++)
		{
			Tri& tri = triplets[i];
			if (tri.row() == row && tri.col() == col)
			{
				val += tri.value();
			}
			else
			{
				if (abs(val) > 1)
				{
					accumlatedTriplets.push_back(Tri(row, col, val));
				}
				row = tri.row(), col = tri.col(), val = tri.value();
			}
		}
		K.setFromTriplets(accumlatedTriplets.begin(), accumlatedTriplets.end());
    }

为了视觉效果，我们需要在一些质点添加定点约束 :

$$p=P^T\hat p+x_0$$

其中, 会从中挑选出非定点坐标，而 包含所有定点坐标，若点为顶点， ，否则 。在求 时需要用完整坐标 。当 更新速度时,需要 将其带入(3.5)并求解线性系统。

4. Finite Element Method

与弹簧质点系统不同，有限元假设一个物体由多个实心小四棱锥构成。每个四棱锥处处密度均匀且相等。

4.1 单个四棱锥

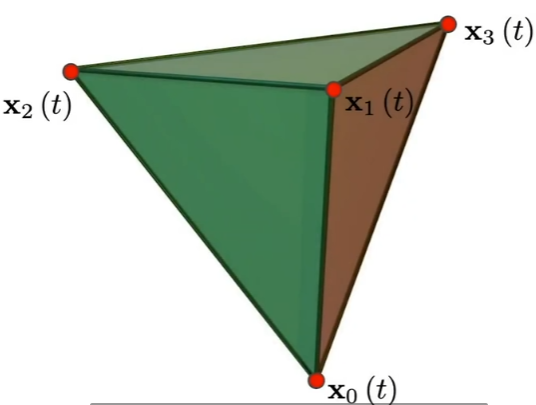
有限元中，系统的动能和势能主要四棱锥的运动和形变产生，这通过对四棱锥内每个质点的位置积分得到。四棱锥每个质点的位置通过其时间 和未形变时位置 的函数描述 。 为质点在 空间的坐标，而 为质点在 空间下的坐标。

对四棱锥的四个顶点 ，可以通过权重 ，描述其内部任意一点坐标

$$x(X,t) =(x_0(t),x_1(t),x_2(t), x_3(t)) \begin{pmatrix} \Phi_0(X)\\ \Phi_1(X)\\ \Phi_2(X)\\ \Phi_3(X) \end{pmatrix} (4.1)$$

该方程在 空间中也成立。对于四棱锥内任意一点 ,加上归一化约束我们能通过求解一下方程得到

$$X= \begin{pmatrix} X_0 & X_1 & X_2 & X_3 \\ 1 & 1 &1 &1 \end{pmatrix} \begin{pmatrix} \Phi_0(X)\\ \Phi_1(X)\\ \Phi_2(X)\\ \Phi_3(X) \end{pmatrix}$$

消去 得到:

$$X-X_0=(X_1-X_0,X_2-X_0,X_3-X_0)\begin{pmatrix} \Phi_1(X)\\ \Phi_2(X)\\ \Phi_3(X) \end{pmatrix}$$ $$\begin{pmatrix} \Phi_1(X)\\ \Phi_2(X)\\ \Phi_3(X) \end{pmatrix}=(X_1-X_0,X_2-X_0,X_3-X_0)^{-1}(X-X_0) (4.2)$$

对每个质点用 (4.2)解出 且给出时刻四顶点坐标后，可用(4.1)求出其在 时刻的位置 。

因此可以用任意时刻四个顶点位置表示系统广义坐标

对(4.1)两边使用向量化算子 ,有:

$$vec(x(X,t))=vec(I_{3\times3} \begin{pmatrix} x_0&x_1&x_2&x_3 \end{pmatrix} \begin{pmatrix} \Phi_0\\ \Phi_1\\ \Phi_2\\ \Phi_3 \end{pmatrix})$$ $$x(X,t)=\begin{pmatrix} \Phi_0\\ \Phi_1\\ \Phi_2\\ \Phi_3 \end{pmatrix}^T \otimes I_{3\times 3} vec(\begin{pmatrix} x_0&x_1&x_2&x_3 \end{pmatrix})=\begin{pmatrix} \Phi_0 I_{3\times3}&\Phi_1I_{3\times3}&\Phi_2I_{3\times3}&\Phi_3I_{3\times3} \end{pmatrix}\begin{pmatrix} x_0\\x_1 \\x_2 \\x_3 \end{pmatrix}=\Phi q (4.3)$$

其中 , 为克罗内克积

对每个四棱锥内质点,其动能有

$$T_q=\frac{1}{2} \rho \dot x^T \dot xd\Omega=\frac{1}{2} \rho \dot q^T \Phi^T\Phi\dot q d\Omega (4.4)$$

其中 为密度,

对(4.4)积分有

$$T=\frac{1}{2} \rho \int_\mathbb{\Omega} \dot q^T \Phi ^T\Phi \dot qd\Omega$$ $$(注意到\dot q与t无关)=\frac{1}{2} \dot q^T \int_\mathbb{\Omega} \Phi^T\Phi d\Omega \dot q$$ $$=\frac{1}{2} \rho \dot q^T \int_\mathbb{\Omega}\begin{pmatrix} \Phi_0 \Phi_0 I_{3 \times 3} & \Phi_0 \Phi_1 I_{3 \times 3} & \Phi_0 \Phi_2 I_{3 \times 3} & \Phi_0 \Phi_3 I_{3 \times 3}\\ \Phi_1 \Phi_0 I_{3 \times 3} & \Phi_1 \Phi_1 I_{3 \times 3} & \Phi_1 \Phi_2 I_{3 \times 3} & \Phi_1 \Phi_3 I_{3 \times 3}\\ \Phi_2 \Phi_0 I_{3 \times 3} & \Phi_2 \Phi_1 I_{3 \times 3} & \Phi_2 \Phi_2 I_{3 \times 3} & \Phi_2 \Phi_3 I_{3 \times 3}\\ \Phi_3 \Phi_0 I_{3 \times 3} & \Phi_3 \Phi_1 I_{3 \times 3} & \Phi_3 \Phi_2 I_{3 \times 3} & \Phi_3 \Phi_3 I_{3 \times 3} \end{pmatrix}d\Omega\dot q=\frac{1}{2} \dot q^TM\dot q\ (4.5)$$

其中积分区域 为reference 空间下的四棱锥, 有:

$$M= \rho \int_\Omega \begin{pmatrix} \Phi_0 \Phi_0 I_{3 \times 3} & \Phi_0 \Phi_1 I_{3 \times 3} & \Phi_0 \Phi_2 I_{3 \times 3} & \Phi_0 \Phi_3 I_{3 \times 3}\\ \Phi_1 \Phi_0 I_{3 \times 3} & \Phi_1 \Phi_1 I_{3 \times 3} & \Phi_1 \Phi_2 I_{3 \times 3} & \Phi_1 \Phi_3 I_{3 \times 3}\\ \Phi_2 \Phi_0 I_{3 \times 3} & \Phi_2 \Phi_1 I_{3 \times 3} & \Phi_2 \Phi_2 I_{3 \times 3} & \Phi_2 \Phi_3 I_{3 \times 3}\\ \Phi_3 \Phi_0 I_{3 \times 3} & \Phi_3 \Phi_1 I_{3 \times 3} & \Phi_3 \Phi_2 I_{3 \times 3} & \Phi_3 \Phi_3 I_{3 \times 3} \end{pmatrix}d\Omega (4.6)$$

动能可以在预计算阶段通过逐个积分 并在模拟过程中带入(4.5)中求得。对单个积分有:

$$\int_\mathbb{\Omega} \Phi_i\Phi_jd\Omega=\int_\mathbb{\Phi} \Phi_i\Phi_j |\frac{\partial \Omega}{\partial \phi}|d\phi$$

其中 积分区域

由(4.2)可得:

$$|\frac{\partial \Omega}{\partial \phi}|=|\begin{pmatrix} X_1 - X_0& X_2-X_0& X_3-X_0 \end{pmatrix}|$$

由行列式的几何意义， 行列式的值为3个列向量构成的平行六面体的体积，也就是3个列向量所构成4棱锥的体积的6倍。

$$|\frac{\partial \Omega}{\partial \phi}|=6vol$$

其中 为四棱锥在reference空间下的体积而:

$$\int_\mathbb{\Omega} \Phi_i\Phi_jd\Omega=6 vol\int_\mathbb{\Phi} \Phi_i\Phi_j d\phi (4.6.1)$$

由于选取的任意性，积分值应关于索引对称，因此:

$$\int_\mathbb{\Phi} \Phi_i\Phi_id\phi=\int_\mathbb{\Phi} \Phi_1^2d\phi=\frac{1}{60}$$ $$(i \ne j)\int_\mathbb{\Phi} \Phi_i\Phi_jd\phi=\int_\mathbb{\Phi} \Phi_1\Phi_2d\phi =\frac{1}{120} (4.6.2)$$

将其带入(4.6)便可求得矩阵

对于系统弹性势能由每个体积微元的形变定义

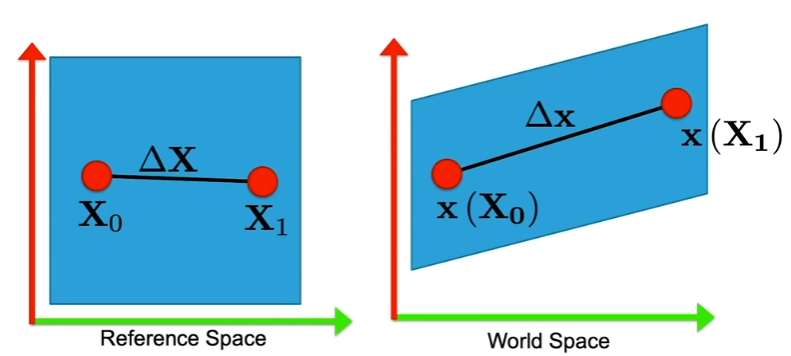
其中在deform 空间下

$$\Delta x=x(X_1,t)-x(X_0,t)$$ $$=x(X_0+\Delta X,t)-x(X_0,t)$$ $$\approx x(X_0,t)+(\frac{\partial x}{\partial X} |_{X_0})\Delta X-x(X_0,t) =(\frac{\partial x}{\partial X}|_{X_0}) \Delta X = F\Delta X (4.7)$$

其中 表示一个体积微元的形变,而函数 描述了该形变下体微元的弹性势能。常用的 为Neohookean Strain Energy Density,课程中使用的形式为:

$$\psi(F)=C(J^{-\frac{2}{3}}tr(F^TF)-3) + D(J-1)^2 (4.8)$$

其中 C,D为材料参数。

令 , 由公式(4.2)和 的线性约束有:

$$\begin{pmatrix} \Phi_1\\ \Phi_2\\ \Phi_3 \end{pmatrix} = T^{-1}(X-X_0) (4.9)$$ $$\Phi_0=1-\Phi_1-\Phi_2-\Phi_3= 1 - \mathbb{1}_3^T\begin{pmatrix} \Phi_1\\ \Phi_2\\ \Phi_3 \end{pmatrix}=1-\mathbb{1}_3^T T^{-1}(X-X_0) (4.10)$$

将(4.9),(4.10)带入(4.1)得

$$x=\begin{pmatrix} x_0 & x_1 & x_2 & x_3 \end{pmatrix} \begin{pmatrix} 1-\mathbb{1}_3^TT^{-1}(X-X_0)\\ T^{-1}(X-X_0) \end{pmatrix}=x_0+\begin{pmatrix} x_0 & x_1 & x_2 & x_3 \end{pmatrix} \begin{pmatrix} -\mathbb{1}_3^TT^{-1}\\ T^{-1} \end{pmatrix}(X-X_0)$$

则 有

$$F=(\frac{\partial x}{\partial X})=\begin{pmatrix} x_0 & x_1 & x_2 & x_3 \end{pmatrix} \begin{pmatrix} -\mathbb{1}_3^TT^{-1}\\ T^{-1} \end{pmatrix}=\begin{pmatrix} x_0 & x_1 & x_2 & x_3 \end{pmatrix} D$$

其中有

两边同时取向量化算子 有:

$$vecF=vec(I_{3\times3} \begin{pmatrix} x_0 & x_1 & x_2 & x_3 \end{pmatrix} D)$$ $$=D^T \otimes I_{3\times3} vec\begin{pmatrix} x_0 & x_1 & x_2 & x_3 \end{pmatrix}$$ $$vecF=\begin{pmatrix} \frac{\partial x}{\partial X} \\ \frac{\partial y}{\partial X}\\ \frac{\partial z}{\partial X}\\ \frac{\partial x}{\partial Y}\\ \frac{\partial y}{\partial Y}\\ \frac{\partial z}{\partial Y}\\ \frac{\partial x}{\partial Z}\\ \frac{\partial y}{\partial Z}\\ \frac{\partial z}{\partial Z} \end{pmatrix}=\begin{pmatrix} d_{00} I_{3\times 3} & d_{10} I_{3\times 3} & d_{20} I_{3\times 3} & d_{30} I_{3\times 3}\\ d_{01} I_{3\times 3} & d_{11} I_{3\times 3} & d_{21} I_{3\times 3} & d_{31} I_{3\times 3} \\ d_{02} I_{3\times 3} & d_{12} I_{3\times 3} & d_{22} I_{3\times 3} & d_{32} I_{3\times 3} \end{pmatrix}\begin{pmatrix} x_0\\ x_1\\ x_2\\ x_3 \end{pmatrix}=Bq (4.11)$$

其中 为四棱锥广义坐标，

而课程中给出的公式为:

$$\begin{pmatrix} \frac{\partial x}{\partial X} \\ \frac{\partial x}{\partial Y}\\ \frac{\partial x}{\partial Z}\\ \frac{\partial y}{\partial X}\\ \frac{\partial y}{\partial Y}\\ \frac{\partial y}{\partial Z}\\ \frac{\partial z}{\partial X}\\ \frac{\partial z}{\partial Y}\\ \frac{\partial z}{\partial Z} \end{pmatrix}=\begin{pmatrix} D_{00}& 0& 0& D_{10}& 0& 0& D_{20}& 0& 0& D_{30}& 0& 0\\ D_{01}& 0& 0& D_{11}& 0& 0& D_{21}& 0& 0& D_{31}& 0& 0\\ D_{02}& 0& 0& D_{12}& 0& 0& D_{22}& 0& 0& D_{32}& 0& 0\\ 0& D_{00}& 0& 0& D_{10}& 0& 0& D_{20}& 0& 0& D_{30}& 0\\ 0& D_{01}& 0& 0& D_{11}& 0& 0& D_{21}& 0& 0& D_{31}& 0\\ 0& D_{02}& 0& 0& D_{12}& 0& 0& D_{22}& 0& 0& D_{32}& 0\\ 0& 0& D_{00}& 0& 0& D_{10}& 0& 0& D_{20}& 0& 0& D_{30}\\ 0& 0& D_{01}& 0& 0& D_{11}& 0& 0& D_{21}& 0& 0& D_{31}\\ 0& 0& D_{02}& 0& 0& D_{12}& 0& 0& D_{22}& 0& 0& D_{32} \end{pmatrix}\begin{pmatrix} x_0\\ x_1\\ x_2\\ x_3 \end{pmatrix}=Bq$$

这里的结论和课程中的不同，原因是这里采用以列为主展开而课程默认以行为主展开。两个结论均正确。潜在能公式可写为:

$$V_\Omega=\psi(F)d\Omega=\psi(Bq)d\Omega$$

对整个reference空间积分，由于 与 无关，因此:

$$V=\int_{\mathbb{\Omega}} \psi(Bq)d\Omega=\psi (Bq) \int_{\mathbb{\Omega}} d\Omega=vol\cdot \psi(Bq)(4.12)$$

对于有多个有限元四棱锥组成的网格体，我们可以用类似弹簧质点系统的方式计算整个系统的动能和势能。

对于整个网格体，其广义坐标为所有顶点的位置 ,为了能单独研究每个四棱锥的能量，定义选择矩阵

$$E_i=\begin{pmatrix} S_{i_0}\\ S_{i_1}\\ S_{i_2}\\ S_{i_3} \end{pmatrix} (4.13)$$

其中 为四棱锥 四个顶点。而根据(4.5)和(4.12)，系统的动能和势能公式能表示为

$$V=\sum_i vol_i \psi(B_iE_iq)(4.14)$$ $$T=\sum_i \frac{1}{2} \dot q^TE_i^TM_iE_i\dot q(4.15)$$

对其求导有:

$$\frac{\partial V}{\partial q} = \sum_i vol_i E_i^TB_i^T \frac{\partial \psi}{\partial F} (4.16)$$ $$\frac{\partial^2 V}{\partial q^2} = \sum_i vol_i E_i^TB_i^T \frac{\partial ^2 \psi}{\partial F^2} B_iE_i (4.17)$$ $$\frac{\partial T}{\partial \dot q}=\sum_i E_i^TM_i^TE_i\dot q=\sum_i E_i^TM_iE_i\dot q(M_i 为对称矩阵)(4.18)$$

5. Backward Implicit Euler Optimization

与弹簧质点类似，我们同样使用backward euler求解有限元:

$$M\dot q^{t+1} = M \dot q ^t+\Delta t f(q^{t+1})$$ $$M \dot q^{t+1}=M \dot q ^t+\Delta t f(q^t + \Delta t \dot q^{t+1}) (5.1)$$

这里 定义为:

$$M=\sum_iE_i^TM_iE_i (5.2)$$

将非线性方程求解问题转为优化问题，令 (5.1)可以写为:

$$Mv=M\dot q^t + \Delta t f(q^t+\Delta tv)$$ $$M(v-\dot q^{t})-\Delta t f(q^t+\Delta t v)=0(5.3)$$

其中由有:

$$\Delta t f(q^t+\Delta t v)=-\Delta t\frac{\partial V}{\partial q} |_{q=q^t+\Delta t v}=-\frac{\partial q}{\partial v} \cdot\frac{\partial V}{\partial q} = -\frac{\partial V}{\partial v} (5.4)$$

则将(5.4)带入(5.3)并对等式左边积分有:

$$E=\int M(v-\dot q^t) + \frac{\partial V}{\partial v} |_{q=q^t + v\Delta t} dv$$ $$=\frac{1}{2}(v-\dot q^t)^TM(v-\dot q^t) + V(q^t+v\Delta t) (5.5)$$

因此，问题转化为:

$$v=arg\min_{v} E (5.6)$$

常见的优化算法见优化算法

对于牛顿法:

$$\frac{\partial E}{\partial v}=M(v-\dot q^t)+\Delta t \frac{\partial V}{\partial q} |_{q=q^t+\Delta tv_i}$$ $$\frac{\partial^2 E}{\partial v^2}=M^T+\Delta t^2\frac{\partial ^2V}{\partial q^2}|_{q=q^t+\Delta t v_i}= M+\Delta t^2\frac{\partial ^2V}{\partial q^2}|_{q=q^t+\Delta t v_i}$$

其中 当前正在搜索的 的值。

6. Cloth(FEM 2D)

和3维FEM类似，2D FEM可用三角形网格表示每个有限元

$$X=\sum_{i\in\{0,1,2\}} X_i \phi_i(X)$$ $$\phi_0=1-\phi_1-\phi_2 = 1-\mathbb{1}^T \begin{pmatrix} \phi_1 \\ \phi_2 \end{pmatrix}$$

这里方程的维度高于未知数的维度，原因在于位置 不一定和 在一个平面上。因此，我们需要让 在平面 上的投影 满足:

$$proj(X)=\sum_{i\in \{0,1,2\}} X_i \phi_i (X)$$ $$\phi_0=1-\phi_1-\phi_2 = 1-\mathbb{1}^T \begin{pmatrix} \phi_1 \\ \phi_2 \end{pmatrix} (6.1)$$

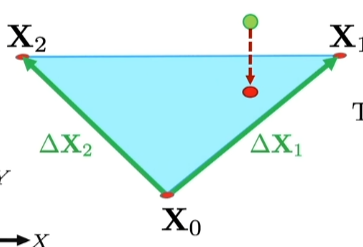
关于如何求得投影值，我们可以将问题转为优化问题解决。令 ,则 在平面上对应点为 到平面的最近点，也就满足:

$$\phi=arg\min_{\phi} E_d=arg\min_{\phi} ||\begin{pmatrix} X_0 &X_1 &X_2 \end{pmatrix} \begin{pmatrix} 1-\mathbb{1^T} \phi\\ \phi \end{pmatrix} -X||_2^2$$ $$=arg\min_\phi||X_0 -X_0\mathbb{1}^T\phi +\begin{pmatrix} X_1 & X_2 \end{pmatrix} \phi - X||_2^2$$

令 , 有

$$E_d=||T \phi-\Delta X||_2^2$$

令 对 求导有:

$$\frac{\partial E_d}{\partial \phi}=\frac{\partial T \phi-\Delta X}{\partial \phi} \cdot2(T \phi-\Delta X)$$ $$=2T^T(T\phi-\Delta X)$$

当 为0时，即为所求:

$$2T^T(T\phi-\Delta X) = 0$$ $$T^TT\phi=T^T\Delta X\to\phi = (T^T T)^{-1}T^T\Delta X (6.2)$$

可用 点在平面的投影坐标 和其到平面的距离 来表示其到有限元顶点的距离函数

$$X=\sum_{i\in \{0,1,2\}} X_i\phi_i(X) +\alpha N=\sum_{i\in{0,1,2}} X_i \phi_i(X) + (X-X_0)^T N\cdot N$$ $$x(t,X)=\sum_{i\in{0,1,2}} x_i(t) \phi_i(X) + ((X-X_0)^TN)\cdot n(t)$$

其中 为平面法线。这种表示方式相比于单纯的三角面片可以表示布料的厚度。

对于系统动能我们有:

$$\frac{1}{2} \rho \int _{\mathbb \Omega}||\dot x||_2^2 d\Omega$$

由于布料很薄。我们可以假定积分值在 上恒定，且布料处处厚度相等。令布料厚度为 :

$$T=\frac{1}{2} \rho h \int_{\mathbb \Omega} || \dot x||_2^2 d\Omega$$

其中积分域 为布料对应的三角形区域。类似(4.3)的推导过程，我们能得到

$$T=\frac{1}{2} \rho h \dot q^T \int_{\Omega} \begin{pmatrix} \phi_0 \phi_0 I_{3\times 3}& \phi_0 \phi_1 I_{3\times 3}& \phi_0 \phi_2 I_{3\times 3}\\ \phi_1 \phi_0 I_{3\times 3}& \phi_1 \phi_1 I_{3\times 3}& \phi_1 \phi_2 I_{3\times 3}\\ \phi_2 \phi_0 I_{3\times 3}& \phi_2 \phi_1 I_{3\times 3}& \phi_2 \phi_2 I_{3\times 3} \end{pmatrix} d\Omega \dot q (6.3)$$

类似(4.6.1),(4.6.2)有:

$$\int _{\Omega} \phi_i\phi_j d\Omega= 2vol\cdot \int_{\mathbb \Phi} \phi_i\phi_j d\phi= \left\{\begin{matrix} 2vol\cdot \frac{1}{12} =\frac{vol}{6} (i=j) \\ 2vol\cdot \frac{1}{24}=\frac{vol}{12} (i\ne j) \end{matrix}\right.$$

TODO…

7. Rigidbody

可用和deformable的FEM类似方法分析刚体。

由于刚体内任意两点的相对距离不会随时间变化:

$$x^Tx-X^TX$$ $$=X^T(F^TF-I)X = 0$$ $$\to F^TF=I , F\in SO(3)$$

因此，我们可以用旋转矩阵 描述刚体的转动:

$$x(t,X)=R(t)X +p (7.1)$$

(7.1)对时间求导有:

$$v=\dot R X+\dot p (7.2)$$

其中 为该点线速度。将(-2.5)带入(7.2)可得:

$$v = R[X]^TR^T\omega + \dot p$$

令广义坐标 带入得:

$$v=R \begin{pmatrix} [X]^T & I \end{pmatrix} \begin{pmatrix} R^T & \\ & R^T \end{pmatrix} \dot q (7.3)$$

利用公式(7.3)可计算刚体内任意一点在世界空间下的线速度 对整个刚体积分，有:

$$T=\frac{1}{2} \int \rho v^T v d\Omega$$ $$=\frac{1}{2} \dot q ^ T \rho \int\begin{pmatrix} R & \\ & R \end{pmatrix} \begin{pmatrix} [X] \\ I \end{pmatrix} R^TR \begin{pmatrix} [X]^T & I \end{pmatrix} \begin{pmatrix} R^T & \\ & R^T \end{pmatrix} d \Omega \dot q$$ $$= \frac{1}{2} \dot q^T \rho \int \begin{pmatrix} R[X][X]^TR^T & R[X]R^T \\ R[X]^TR^T & I \end{pmatrix} d\Omega \dot q$$ $$=\frac{1}{2} \dot q^T \begin{pmatrix} \int \rho R[X][X]^TR^T d\Omega & \int \rho R[X]R^T d\Omega \\ \int \rho R[X]^TR^T d\Omega & \int \rho d \Omega I \end{pmatrix} \dot q (7.4)$$

为了方便研究，取reference space下的坐标为 ,质心坐标 满足 ,则:

$$\int \rho [\bar{X}] d\Omega$$ $$=\int\rho ([X] - [C] ) d\Omega\\ = \int \rho [X] d\Omega - \int \rho d\Omega [C]\\ = \int \rho [X] d \Omega - \int \rho d\Omega \cdot \frac{\int \rho [X] d\Omega}{\int \rho d\Omega} = 0 (7.5)$$

将(7.5)带入(7.4)得:

$$T=\frac{1}{2} \dot q^T \begin{pmatrix} \int \rho R[\bar X][\bar X]^TR^T d\Omega & O \\ O & \int \rho d \Omega I \end{pmatrix} \dot q$$

其中:

$$\int \rho [\bar X][\bar X]^T d\Omega = \int \rho \begin{pmatrix} y^2 + z^2 & -xy & -xz\\ -xy & x^2 + z^2 & -yz\\ -xz &-yz & x^2 + y^2 \end{pmatrix} d \Omega = \mathbb{I} (7.6)$$

为刚体转动惯量

$$\int \rho d\Omega I=mI (7.7)$$

为刚体质量。带入(7.5)得:

$$T= \frac{1}{2} \dot q ^T \begin{pmatrix} R \mathbb{I} R^T & O \\ O & mI \end{pmatrix} \dot q = \frac{1}{2} w^T R\mathbb{I}R^T w + \frac{1}{2} m\dot q^T \dot q$$

由于刚体无形变，弹性势能为0。因此，系统潜在能

带入(1.3)得（这公式我不会推，直接抄结论）:

$$(R\mathbb{I}R^T) \dot w=w\times (R\mathbb{I}R^T) w+ \tau_{ext} (7.8)$$ $$m\ddot{p} = f_{ext} (7.9)$$

其中 为系统外力， 为系统外力矩。

得到 的显式更新公式:

$$(R\mathbb{I}R^T) w^{t+1} = (R\mathbb{I}R^T) w^t + \Delta t w\times (R\mathbb{I}R^T) w + \Delta t \tau_{ext} (7.9)$$ $$\dot p^{t+1} = \dot p^{t} + \frac{1}{m} f_{ext} \Delta t (7.10)$$

由于 有:

$$\frac{dx}{dt}= [w]x,x_{t_0} = x_0$$ $$x=e^{[w]\Delta t}x_0$$ $$x^{t+1}=e^{[w]\Delta t} R^t \bar X$$

则:

$$R^{t+1} = e^{[w]^t \Delta t} R^t (7.11)$$ $$p^{t +1} = p^t + \dot p^{t} \Delta t (7.12)$$

9.Rigidbody Contact

对于单刚体系统，其速度更新公式为:

$$(R\mathbb{I}R^T)w^{t + 1}= (R\mathbb{I}R^T) w^{t} + w^t\times (R\mathbb{I}R^T)w^t \Delta t + \tau_{ext} \Delta t$$ $$mI\dot p^{t+1} = mI\dot p^{t} + f_{ext} \Delta t$$

整理后有:

$$M\dot q^{t+1}=M\dot q^{t} + f\Delta t (9.1)$$

其中:

$$M= \begin{pmatrix} R\mathbb{I}R^T & \\ & mI \end{pmatrix}$$ $$\dot q= \begin{pmatrix} w \\ \dot p \end{pmatrix}$$ $$f= \begin{pmatrix} w^t\times R\mathbb{I}R^Tw^t + \tau_{ext} \\ f_{ext} \end{pmatrix}$$

对于双刚体系统当两刚体相撞时有:

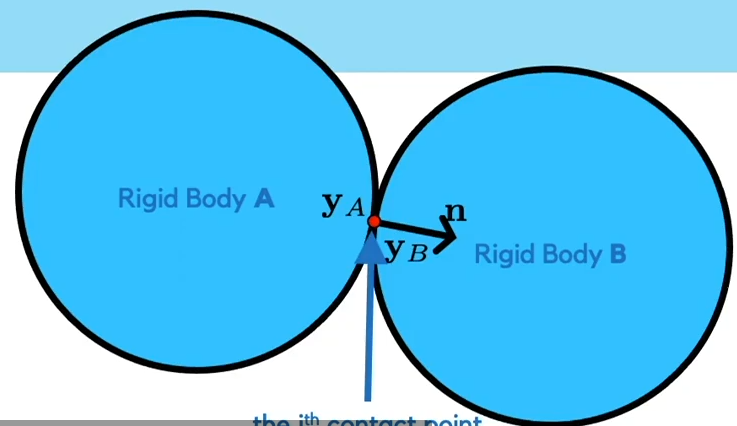
撞击点, 同理。

撞击处的应力 其中, 为力度大小, 为撞击点法线的反方向。

将 转到reference space,求解reference space下的力矩:

$$\tau_{ref} = \bar X \times (R_A^T f)=[\bar X] R^T_A f$$

将该力矩转到world space有:

$$\tau = R_A[\bar X]R_A^T f=\alpha R_A[\bar X] R_A^T n_A$$

则对刚体A除了外力 和外力矩 ,应存在撞击处的力和力矩。将 带入(9.1)中有:

$$M\dot q^{t+1}=M\dot q^{t} + f_{ext}\Delta t + \begin{pmatrix} \alpha R [\bar X]R^Tn \\ \alpha n \end{pmatrix}=M\dot q + f_{ext} \Delta t + \alpha \begin{pmatrix} R & \\ & R \end{pmatrix} \begin{pmatrix} [X] \\ I \end{pmatrix} R^T n (9.2)$$

由(7.3)有:

$$J=R \begin{pmatrix} [X]^T & I \end{pmatrix} \begin{pmatrix} R^T & \\ & R^T \end{pmatrix} (9.3)$$

为 的Jacobian 矩阵。对任意广义速度 有:

$$v(t,X)=J(X)\dot q^t (9.4)$$

将(9.3)带入(9.2)中得到:

$$M\dot q_A^{t+1} = M\dot q_A^t + f_{ext} \Delta t + \alpha J_A ^T(y) n(9.5)$$

对于多刚体系统

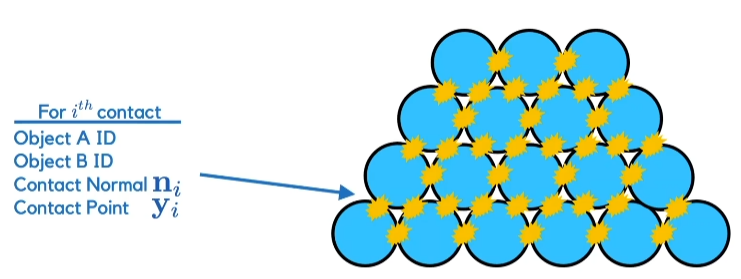
每个刚体有多个接触点,（9.5）可以变形为:

$$M\dot q_A^{t+1} = M \dot q_A ^t + f_{ext} \Delta t +\sum_i \alpha_i J_A(y_i)^Tn_i (9.6)$$

其中A为研究的当前刚体， 为刚体 的第个接触点。刚体 与 在点i接触

(9.6)需满足约束:

$$\alpha_i \ge 0(9.7.1)$$ $$n_i^T (\dot y_B^{t+1}-\dot y_A^{t+1}) \ge 0 (9.7.2)$$ $$n_i^T(\dot y_B^{t+1} - \dot y_A^{t+1}) \perp \alpha_i (9.7.3)$$

令 则:

$$M\dot q_A^{t+1} = M\dot q_A^t + f_{ext} \Delta t + \sum_i \Delta t\alpha_i g_i^A (9.8)$$

对单个接触点i将其与其它接触点分离有:

$$M\dot q_A^{t+1} = M\dot q_A^t + f_{ext} \Delta t + \sum_{j\ne i} \Delta t \alpha_j g_j^A + \Delta t\alpha _i g_i^A$$ $$\dot q_A^{t+1} = \dot q_A^t + f_{ext}M^{-1} \Delta t + M^{-1}\sum_{j\ne i} \Delta t \alpha_j g_j^A + M^{-1}\Delta t\alpha _i g_i^A$$ $$\dot q_A^{t+1} = \dot q^*_A+ \Delta t M^{-1} f_i^A + \Delta t \alpha_i M^{-1}g_i^A (9.9)$$

其中 为系统未约束速度,而 为系统约束产生的速度其中 为系统除接触点i外对刚体A产生的约束力

将公式(7.3)带入约束(9.7.2)得:

$$n_i^T(J_B(y_i)\dot q_B^{t+1} - J_A(y_i)\dot q_A^{t+1}) \ge 0$$ $$由于n_i^A=-n_i,n_i^B=n_i\to (g_i^B)^T\dot q_B^{t+1} + (g_i^A)^T\dot q_A^{t+1} \ge 0 (9.10)$$

将公式(9.9)带入约束(9.10)得:

$$\Delta t [(g_i^A)^TM_A^{-1} g_i^A+(g_i^B)^TM_B^{-1} g_i^B] \alpha_i +(g_i^B)^T(\dot q_B^*+\Delta t M_B^{-1} f_i^B) + (g_i^A)^T (\dot q_A^* + \Delta t M_A^{-1} f_i^A) \ge0$$

令 ,$\gamma_i = (g_i^B)^T(\dot q_B^+\Delta t M_B^{-1} f_i^B) + (g_i^A)^T (\dot q_A^ + \Delta t M_A^{-1} f_i^A)$ 则约束(9.7)可变为:

$$\alpha_i \ge 0 (9.11.1)$$ $$\delta_i \alpha_i+\gamma_i\ge 0 (9.11.2)$$ $$\delta_i \alpha_i + \gamma_i \perp \alpha_i (9.11.3)$$

解得:

$$\alpha_i = \left\{\begin{matrix} \frac{-\delta_i }{\gamma_i} , \frac{-\delta_i}{\gamma_i}\ge 0 \\ 0,\frac{-\delta_i}{\gamma_i}\le 0 \end{matrix}\right. (9.12)$$

对于整个系统，可利用Projected Gauss-Seidel法求解线性方程组(9.11.2):

1. 对系统所有contact,初始化
2. 进入循环，直到 满足 约束(9.11)
   1. 循环遍历每个contact点:
      1. 根据当前 计算,
      2. 将, 带入(9.12)中，计算

关于Gauss-Seidel详细说明可以看Appx 4

Appx 2. Time Derivative of Rotation Matrix

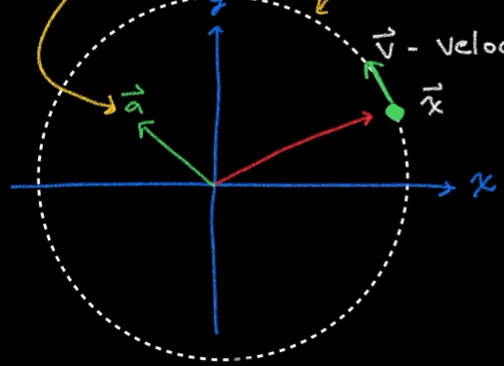
绕轴 旋转的质点 的线速度为:

$$v = \alpha d = tan(\frac{\partial \theta}{\partial t} \Delta t) ||x||\frac{a \times x}{||x||}=\dot{\theta} a\times x (-2.1)$$

定义向量 为质点的角速度 有:

$$v=\omega \times x (-2.2)$$

将 写成矩阵相乘形式带入(-2.2)中有:

$$\frac{d x}{d t}=v=\begin{pmatrix} 0& - w_z & w_y \\ w_z & 0 & -w_x\\ - w_y & w_x & 0 \end{pmatrix} x =[w]x$$

解该常微分方程，得:

$$x(t)=e^{[w]t} x (-2.3)$$

( )

$$\dot{x}(t)=[w]e^{[w]t}x=[w]x(t)=\dot{R}x$$

则当 极小时:

$$\dot{R}=[w]$$ $$R = [w]x$$

对任意时刻:

$$x(t+\Delta t)=\Delta R(\Delta t) x(t)=\Delta R(\Delta t) R(t) x_0$$ $$v = \frac{d x}{d\Delta t}=\Delta \dot{ R}(\Delta t) R(t) x_0=[w]R(t) x_0 (-2.4)$$

(-2.4)有:

$$v=[w] R(t)x_0$$ $$=w\times R(t) x_0$$ $$=-(R(t)x_0) \times w$$ $$= -R(t)(x_0\times R^{-1}(t) w)$$ $$=-R(t)(x_0\times R^{T} (t) w)$$ $$=R(t)(-[x_0])R^{T} (t) w=R(t)[x_0]^T R^T(t) w (-2.5)$$

Appx 4 Gauss-Seidel and Rigidbody Contact Solving

TODO: